Was ist ein Algorithmus? – Eine Definition

Algorithmus Erklärung

Ein Algorithmus ist ein Verfahren oder eine Formel zur Lösung eines Problems, das auf der Durchführung einer Abfolge bestimmter Aktionen beruht. Ein Computerprogramm kann als ein ausgeklügelter Algorithmus betrachtet werden. In der Mathematik und Informatik bezeichnen Algorithmen in der Regel ein kleines Verfahren, das ein wiederkehrendes Problem löst.

Algorithmen sind in allen Bereichen der IT (Informationstechnologie) weit verbreitet. Algorithmen für eine Suchmaschine zum Beispiel nehmen Suchbegriffe und Operatoren als Eingabe, durchsuchen die zugehörige Datenbank nach relevanten Webseiten und geben die Ergebnisse zurück.

Ein Verschlüsselungsalgorithmus wandelt Daten nach bestimmten Aktionen um, um sie zu schützen. Ein Algorithmus mit geheimem Schlüssel, wie der Data Encryption Standard (DES), verwendet beispielsweise denselben Schlüssel zur Ver- und Entschlüsselung von Daten.

Man kann sich Algorithmen leicht als Flussdiagramm vorstellen. Die Eingabe führt zu Schritten und Fragen, die der Reihe nach bearbeitet werden müssen. Wenn jeder Abschnitt des Flussdiagramms abgeschlossen ist, ist das erzeugte Ergebnis die Ausgabe.

Solange der Algorithmus ausreichend ausgeklügelt ist, kann niemand, der den Schlüssel nicht kennt, die Daten entschlüsseln.

Das Wort Algorithmus leitet sich vom Namen des Mathematikers Mohammed ibn-Musa al-Khwarizmi ab, der dem königlichen Hof in Bagdad angehörte und von etwa 780 bis 850 lebte. Al-Khwarizmis Arbeit ist wahrscheinlich auch die Quelle für das Wort Algebra.

Algorithmen und Automatisierung

Das hört sich soweit ganz einfach an, aber wofür wird ein Algorithmus verwendet? Die Antworten sind sehr vielfältig.

Ein gutes Beispiel für Algorithmen in Aktion ist die Automatisierungssoftware. Automatisierungssoftware funktioniert nämlich nach bestimmten Regeln, um Aufgaben zu erfüllen. Diese Regeln bilden einen Algorithmus.

Automatisierungssoftware besteht also aus vielen Algorithmen, die alle darauf abzielen, Prozesse zu automatisieren.

Eine Ihrer automatisierten Aufgaben besteht beispielsweise darin, dass Ihre Automatisierungssoftware alle per E-Mail eingegangenen Rechnungsdaten in ein Arbeitsblatt einträgt. Dazu stellen Sie eine Reihe von Regeln und Bedingungen auf, die das Programm befolgen soll – einen Algorithmus.

In diesem Fall ist die Eingabe jede eingehende E-Mail. Jede dieser E-Mails durchläuft dann die einzelnen Schritte – oder Regeln -, um die Aufgabe zu erfüllen. Dazu kann das Scannen jeder E-Mail nach Schlüsselbegriffen gehören. E-Mails, die diese Begriffe enthalten, werden dann zum nächsten Schritt weitergeleitet, und jeder Schritt wird fortgesetzt, um die relevanten Daten zu identifizieren und zu extrahieren. Das Ergebnis sind die Informationen, die in ein Arbeitsblatt eingefügt werden.

Beispiele für Algorithmen

Hier ist eine Liste der unterschiedlichen Arten von Algorithmen:

• Brute-Force-Algorithmus
• Greedy-Algorithmus
• Rekursiver Algorithmus
• Backtracking-Algorithmus
• Divide & Conquer-Algorithmus
• Dynamischer Programmieralgorithmus
• Randomisierter Algorithmus

Brute-Force-Algorithmus

Der einfachste Algorithmus, der zur Lösung eines Problems entwickelt werden kann, wird als Brute-Force-Algorithmus bezeichnet. Um eine optimale Lösung zu finden, müssen wir zunächst eine Lösung finden und dann versuchen, sie zu optimieren. Jedes Problem kann mit dem Brute-Force-Verfahren gelöst werden, wenn auch im Allgemeinen nicht mit nennenswerter Raum- und Zeitkomplexität.

Greedy-Algorithmus

Bei diesem Algorithmus wird eine Entscheidung getroffen, die zu diesem Zeitpunkt gut ist, ohne die Zukunft zu berücksichtigen. Das bedeutet, dass ein lokaler Bestwert gewählt wird, der als das globale Optimum angesehen wird. Er zeichnet sich durch zwei Eigenschaften aus.

• Auswahl der besten Option aus Kostengründen.
• Optimale Substruktureigenschaft: Wenn eine optimale Lösung gefunden werden kann, indem man die optimale Lösung für seine Unterprobleme findet.

Der Greedy-Algorithmus funktioniert nicht immer, aber wenn er funktioniert, dann funktioniert er wie ein Zauber! Dieser Algorithmus ist einfach zu handhaben und meistens der einfachste. Aber das Treffen der lokal besten Entscheidungen funktioniert nicht immer so, wie es sich anhört. Daher wird er durch eine zuverlässige Lösung namens Dynamische Programmierung ersetzt.

Anwendungen:

• Sortieren: Auswahlsortierung, Topologische Sortierung
• Prim’s & Kruskal’s Algorithmen
• Problem des Geldwechsels
• Fractional Knapsack Problem
• Job Scheduling Algorithmus

Zum besseren Verständnis gehen wir das häufigste Problem durch, nämlich das Job Scheduling Problem: Betrachten wir eine Situation, in der uns die Anfangs- und Endzeiten verschiedener Veranstaltungen in einem Auditorium gegeben sind. Ihre Aufgabe besteht nun darin, die Anzahl der Veranstaltungen zu maximieren, die im Hörsaal organisiert werden können, wobei sich keine zwei Veranstaltungen überschneiden dürfen (die Anfangs- oder Endzeit einer Veranstaltung liegt nicht zwischen dem Anfangs- und Endpunkt einer anderen Veranstaltung).

Wir betrachten sechs solcher Veranstaltungen:

	A	B	C	D	E	F
Beginn	1	2	5	4	3	6
Ende	6	3	9	6	5	10

Wenn wir die Ereignisse nach ihren Anfangszeiten sortieren und mit dem ersten Ereignis beginnen, während wir alle Ereignisse ausschließen, die sich mit den vorherigen überschneiden, wird dies sicherlich zu einer Lösung führen, aber es wird die Anzahl der Ereignisse nicht maximieren. Nach der Sortierung nach der Anfangszeit sehen wir Folgendes:

	A	B	C	D	E	F
Beginn	1	2	3	4	5	6
Ende	6	3	5	6	9	10

Die Ereignisse, die organisiert werden können, sind also A bis F. Unser Brute-Force-Ansatz wird also mehrere solcher Fälle haben und scheitern, wenn wir nicht das optimale Anfangsereignis auswählen. Sehen wir uns nun an, was unser Greedy-Algorithmus vorschlägt. Nach dem Greedy-Algorithmus sortieren wir die Ereignisse nach ihren Endzeiten, d. h. wir wählen die Ereignisse aus, die zuerst enden. Unsere neue Ereignistabelle wird wie folgt aussehen:

	B	E	A	D	C	F
Beginn	2	3	1	4	5	6
Ende	3	5	6	6	9	10

Wir wählen also – B, E, C, was sicherlich eine größere Anzahl von Ereignissen ist als zuvor. Daher bietet der Greedy-Algorithmus in solchen Fällen die beste Lösung für diese Art von Problem.

Rekursiver Algorithmus

Dies ist einer der am einfachsten zu entwickelnden Algorithmen, da es nicht erforderlich ist, über jedes Teilproblem speziell nachzudenken. Das bedeutet, dass wir nur über die vorhandenen Fälle und die Lösung des einfachsten Teilproblems nachdenken müssen, alle anderen Komplexitäten werden automatisch behandelt.

Die Rekursion ist ein sehr mächtiges Werkzeug, obwohl wir hier immer auf die Speicherverwaltung achten sollten, da die Rekursion mit einem rekursiven Stack arbeitet, der jedes Mal aufgerufen wird, wenn die Rekursionsfunktion aufgerufen wird. Rekursion bedeutet einfach, sich selbst aufzurufen, um seine Unterprobleme zu lösen.

Zum Beispiel:

// Fakultät einer Zahl
int Fact(x) {

if (x==0) return 1;

turn x*Fact(x-1);

}

Zeitkomplexität: O(n)
Denken Sie jedoch immer daran, den Basisfall anzugeben, da die Schleife sonst bis ins Unendliche fortgesetzt wird und Speicherfehler verursacht. Dieser Algorithmus ist einfacher zu entwerfen und zu implementieren.

Backtracking-Algorithmus

Dies ist eine Verbesserung des Brute-Force-Ansatzes. Hier beginnen wir mit einer von vielen möglichen Optionen und versuchen, das Problem zu lösen. Wenn wir in der Lage sind, das Problem mit dem gewählten Zug zu lösen, geben wir die Lösung aus, andernfalls gehen wir zurück, wählen eine andere Option und versuchen, sie zu lösen. Es handelt sich um eine Form der Rekursion, nur dass wir, wenn eine gegebene Option keine Lösung ergibt, zur vorherigen Option zurückgehen, die eine Lösung ergeben kann, und mit anderen Optionen fortfahren.

Anwendungen:

• Generierung aller binären Zeichenketten
• N-Queens-Problem
• Knapsack-Problem
• Graphenfärbungsproblem

Sehen wir uns die Anwendung dieses Algorithmus bei der Erzeugung aller Zeichenketten mit n Bits an.

// Funktion für ein Backtracking Problem
int Array[N];
Binary(int N) {

if(N < 1)

printf(„%s“, Array;)

else {

Array[N-1] = 0;
Binary(N-1);
Array[N-1] = 1;
Binary(N-1);

}

}

Zeitkomplexität: 0(2^N)

Divide & Conquer-Algorithmus

Dies ist einer der am häufigsten verwendeten Algorithmen in der Programmierung. Bei diesem Algorithmus werden die Probleme in Teilprobleme unterteilt, die dann einzeln gelöst und anschließend zur Lösung der gegebenen Probleme kombiniert werden.

Auch hier ist es nicht möglich, alle Probleme mit diesem Verfahren zu lösen. Wie der Name schon sagt, besteht er aus zwei Teilen: Teilen des Problems in Teilprobleme auf und bearbeiten dieser Teilprobleme.

Kombinieren Sie die Lösungen der einzelnen Teilprobleme.
Diese Algorithmen werden häufig für verschiedene Probleme verwendet, da sie recht stabil arbeiten und für die meisten der gestellten Probleme optimal sind.

Das gegebene Problem wird in zwei Teile von n/a und n/b Größe aufgeteilt und dann separat und rekursiv berechnet, um das Ergebnis zurückzugeben und sie zu kombinieren, um die Lösung zu bilden.

Anwendungen:

• Binäre Suche
• Merge-Sortierung & Schnellsortierung
• Median-Suche
• Matrix-Multiplikation

Lassen Sie uns die einfachste Anwendung der binären Suche besprechen. Zuvor haben wir beschrieben, wie die Suche nach einem Element in einem sortierten Array O(n) Zeit in Anspruch nimmt. Diesmal wenden wir den Divide-and-Conquer-Algorithmus an, um seine Komplexität auf O(logn) zu reduzieren.

//Binäre Suche
bool find_element(int_arr[],int srch,in si,int ei) {

if(si>ei) return false;
int mid = si + (ei-si)/2;
if(arr[mid]==srch) return true;
if(arr[mid]<srch)

return find_element(arr,srch,mid+1,ei);

if(arr[mid]>srch)

return find_element(arr,srch,si,mid-1);

return false;

}
int main()
{

int arr[] = {1,2,3,5,6,8};
int srch = 5;
bool searching = find_element(arr,srch,0,5);
cout<<<searching;
return 0;

}

Output 1:

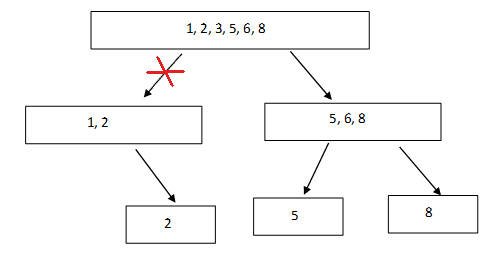
Der Programmfluss bewegt sich zum rechten Unterfeld, da fünf größer ist als die aktuelle Mitte (3), und iteriert daher nicht über die Hälfte der Elemente, was die Zeitkomplexität verringert. Obwohl dies nicht anwendbar ist, wenn das Array nicht sortiert ist, wird es nur einen Teil des Arrays vernachlässigen und der Algorithmus wird fehlschlagen.

Dynamischer Algorithmus

Dieser gehört zu de beliebtesten Algorithmen, da er die effizienteste Methode zur Lösung eines Problems bietet. Es bedeutet einfach, dass man sich an die Vergangenheit erinnert und sie auf die entsprechenden Ergebnisse in der Zukunft anwendet, weshalb er in Bezug auf die Zeitkomplexität recht effizient ist.

Die dynamische Programmierung bietet zwei Vorteile:

• Optimale Substruktur: Eine optimale Lösung für ein Problem enthält eine optimale Lösung für seine Teilprobleme.
• Überlappende Teilprobleme: Eine rekursive Lösung enthält eine kleine Anzahl von unterschiedlichen Teilproblemen.

Und hat zwei verschiedene Ausprägungen:

• Bottom-Up-Ansatz: Beginnt mit der Lösung von unten nach oben, d. h. er löst zuerst das letztmögliche Teilproblem und verwendet das Ergebnis dieser Lösung für die darüber liegenden Teilprobleme.
• Top-Down-Ansatz: Beginnt mit der Lösung der Probleme von Anfang an, um zu dem gewünschten Teilproblem zu gelangen, und löst es mit Hilfe der zuvor gelösten Teilprobleme.

Anwendungen:

• Längste gemeinsame Folge, längste ansteigende Folge, längste gemeinsame Teilfolge usw.
• Bellman-Ford-Algorithmus
• Ketten-Matrix-Multiplikation
• Teilmengensumme
• Knapsack-Problem & viele mehr.

Randomisierter Algorithmus

Dies ist ein Algorithmus, der seine Entscheidungen auf der Grundlage von Zufallszahlen trifft, d. h. er verwendet Zufallszahlen in seiner Logik.

Das beste Beispiel hierfür ist die Wahl des Pivot-Elements in Quicksort. Diese Zufälligkeit dient dazu, die Zeit- oder Raumkomplexität zu verringern, wird aber nicht regelmäßig verwendet. Die Wahrscheinlichkeit spielt hier die wichtigste Rolle.

Wenn wir bei Quicksort nicht das richtige Element wählen, haben wir im schlimmsten Fall eine Laufzeit von O(n^2 ). Bei richtiger Auslegung kann die beste Laufzeit von O(nlogn) erreicht werden.

Anwendungen:

• Randomisierte Schnellsortierung
• Kager’s Algorithmus usw.

 

Letztes Update des Artikels: 20. September 2021