Leistungsfaktor berechnen & Leistungsfaktor Rechner

Der Leistungsfaktor Rechner

Dieser Leistungsfaktor Rechner ist ein praktisches Werkzeug zur Analyse des in elektrischen Schaltkreisen fließenden Wechselstroms (AC). Wahrscheinlich ist schon bekannt, dass man den Gleichstrom (DC) mit Hilfe des Ohm’schen Gesetzes berechnen kann. Im Falle von Wechselstrom ist diese Funktion nicht so einfach, da solche Schaltungen sowohl Wirkleistung als auch Blindleistung enthalten.

Dieser Rechner hilft nicht nur dabei, die Werte der verschiedenen Leistungsarten in der Schaltung herauszufinden, sondern liefert auch eine Formel für den Leistungsfaktor, die das Verhältnis zwischen der Wirk- und der Scheinleistung ausdrückt.

Leistungsfaktor-Rechner

 

Wirk-, Blind- und Scheinleistung

Wenn man verstehen will, was der Leistungsfaktor ist, braucht man zunächst ein tieferes Verständnis seiner Komponenten: der Wirkleistung, der Blindleistung und der Scheinleistung.

Wirkleistung

Die Wirkleistung, auch als Realleistung bekannt und durch das Symbol P repräsentiert, spielt eine entscheidende Rolle bei der Umwandlung elektrischer Energie in effektive Arbeit in einem Schaltkreis. Im Wesentlichen erfolgt die Umsetzung der Wirkleistung hauptsächlich in ohmschen Widerständen. Ein charakteristisches Merkmal der Wirkleistung ist ihre Präsenz in Gleichstromkreisen, wo sie als einzige Leistungsform auftritt.

Im Gegensatz dazu durchlaufen die Werte von Strom und Spannung in einem Wechselstromkreis sinusförmige Änderungen. Die Einheit der Wirkleistung ist das Watt (W), und sie stellt eine grundlegende Größe dar, um die tatsächliche Leistung in einem elektrischen System zu quantifizieren.

Blindleistung

Die Blindleistung, dargestellt durch das Symbol Q, tritt auf, wenn Strom und Spannung im Wechselstromkreis um 90 Grad phasenverschoben sind. In solchen Fällen wird keine Nettoenergie in Form von Wirkleistung übertragen, und die Blindleistung ermöglicht keine direkte Ausführung von Arbeit. Im Gegensatz zur Wirkleistung ist Blindleistung in Gleichstromkreisen nicht vorhanden.

Sie ist eng mit der Reaktanz von Induktivitäten und Kondensatoren verbunden, was wiederum zu einer Verschiebung der Phasenlage führt. Die Maßeinheit der Blindleistung lautet Volt-Amps-Reactive (VAR), und ihre Existenz ist entscheidend für die Aufrechterhaltung eines ausgewogenen Leistungsfaktors in Wechselstromsystemen.

Scheinleistung

Die Scheinleistung, durch das Symbol S repräsentiert, ist eine umfassende Größe, die die kombinierten Effekte von Wirkleistung und Blindleistung in einem elektrischen System berücksichtigt. Sie wird als das Produkt der Effektivwerte von Spannung und Strom in der Schaltung berechnet. Interessanterweise ignoriert die Scheinleistung den Phasenwinkel zwischen Strom und Spannung und wird in Volt-Ampere (VA) gemessen.

Es ist wichtig zu betonen, dass die Scheinleistung nicht direkt zur Ausführung von mechanischer Arbeit genutzt wird. Vielmehr dient sie als Kennzahl für die gesamte Leistung im System, indem sie die vektorielle Summe von Wirk- und Blindleistung darstellt. In der Praxis ist die Scheinleistung ein Schlüsselkonzept für die Beurteilung der Leistungsfähigkeit und Effizienz von elektrischen Systemen.

Das Leistungsdreieck der Elektrotechnik

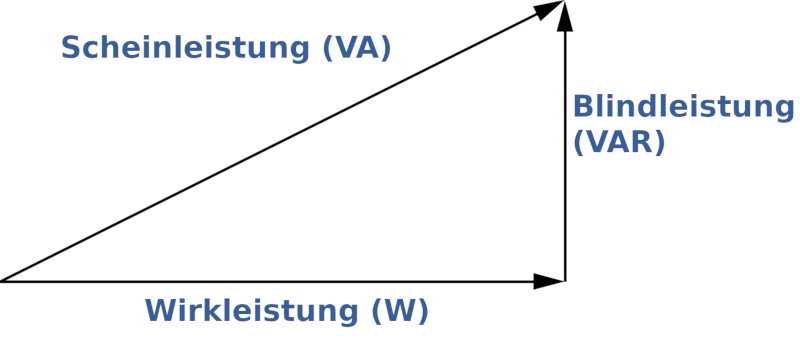
Da die Scheinleistung durch vektorielle Addition der Wirk- und Blindleistung ermittelt werden kann, kann man diese drei Werte mit einer grafischen Methode in Form eines Dreiecks, dem sogenannten Leistungsdreieck, darstellen.

Jede Seite des Dreiecks repräsentiert eine der drei Formen von Energie, die in einem Wechselstromkreis übertragen wird. Die Schenkel des rechtwinkligen Dreiecks stellen die Wirk- und Blindleistung und die Hypotenuse – die Scheinleistung – dar.

Eine der Folgen der Verwendung des Machtdreiecks ist, dass die mathematische Beziehung zwischen den drei Werten mit Hilfe des Satzes des Pythagoras leicht hergestellt werden kann:

S² = P² + Q²

Zusätzlich ist der Winkel zwischen der Wirkleistung und der Scheinleistung, der mit φ bezeichnet wird, der Impedanzphasenwinkel der Schaltung.

Die Leistungsfaktor Formel

Der Leistungsfaktor ist das Verhältnis zwischen Wirk- und Scheinleistung in einem Stromkreis. Wenn keine Blindleistung vorhanden ist, dann ist der Leistungsfaktor gleich 1, wenn dagegen die Wirkleistung gleich Null ist, dann ist auch die Scheinleistung gleich 0.

Die Formel des Leistungsfaktors lautet:

Leistungsfaktor = P / S

Zum Beispiel bedeutet ein Leistungsfaktor von 0,87, dass 87 % des Stroms, welchen man dem Stromkreis zuführt, echte Arbeit leistet. Der Rest der Leistung – 13%, um genau zu sein – muss bereitgestellt werden, um die Blindleistung auszugleichen.

Natürlich kann zur Berechnung des Leistungsfaktor aber auch unser einfacher Leistungsfaktor Rechner genutzt werden!

Wie wird der Leistungsfaktor berechnet?

Der Leistungsfaktor kann auch mit Hilfe des Leistungsdreiecks berechnet werden. Nach den Prinzipien der Trigonometrie kann man ihn folgendermaßen festlegen:

P / S = cos φ

Da der Leistungsfaktor gleich dem Verhältnis zwischen Wirk- und Scheinleistung ist,

Leistungsfaktor = cos φ

Das bedeutet, dass bei Kenntnis nur eines von drei Werten – Wirkleistung, Blindleistung oder Scheinleistung – und entweder des Leistungsfaktors oder des Phasenwinkels schnell die restlichen dieser Werte berechnet werden können, die einen Wechselstromkreis definieren. Anstatt die Zahlen manuell einzugeben, genügt es natürlich, diesen Leistungsfaktor-Rechner zu verwenden!

Der Leistungsfaktor, ein entscheidender Parameter in der Analyse von Wechselstromkreisen, kann mithilfe des Leistungsdreiecks und trigonometrischer Prinzipien bestimmt werden. Die Gleichung P / S = cos φ verdeutlicht diese Beziehung, wobei φ der Phasenwinkel zwischen Wirk- und Scheinleistung ist.

Trigonometrische Interpretation:

Die trigonometrische Interpretation des Leistungsfaktors ermöglicht eine tiefere Einsicht in die Beziehung zwischen Wirk- und Scheinleistung. Cos φ repräsentiert das Verhältnis von Wirk- zu Scheinleistung. Eine präzise Berechnung des Leistungsfaktors ist somit möglich, wenn einer der drei Werte bekannt ist. Diese trigonometrische Perspektive erleichtert die schnelle Bestimmung aller relevanten Größen und verdeutlicht die Bedeutung des Phasenwinkels in der Charakterisierung von Wechselstromkreisen.

Widerstand, Reaktanz und Impedanz

Die drei Hauptbestandteile eines Wechselstromkreises sind Widerstände, Kondensatoren und Induktivitäten. Mit diesem Leistungsfaktor-Rechner können nicht nur die Leistung beschrieben werden, die durch jede dieser Komponenten übertragen wird, sondern auch festgestellt werden, was passiert, wenn ein elektrischer Strom durch sie fließt – nämlich welcher Widerstand, Reaktanz und Impedanz diese Elemente besitzen.

Der Widerstand, bezeichnet mit R und ausgedrückt in Ohm (Ω), ist das Mass dafür, um wie viel ein Leiter (vor allem ein Widerstand) den durch ihn fliessenden elektrischen Strom I reduziert. Dieser Wert steht in direktem Zusammenhang mit der in einem Wechselstromkreis fliessenden Wirkleistung. Diese Beziehung kann als P = I²R geschrieben werden.

Die Reaktanz, die mit X bezeichnet und auch in Ohm gemessen wird (Ω), ist die Trägheit, die der Bewegung von Elektronen in einer Schaltungskomponente entgegenwirkt. Sie ist hauptsächlich in Kondensatoren und Induktivitäten vorhanden. Wenn man einen Wechselstrom durch eine Komponente mit hoher Reaktanz laufen lässt, ist der Spannungsabfall um 90 Grad phasenverschoben mit dem Strom. Die Reaktanz ist mit der Blindleistung durch die Gleichung Q = I²X verknüpft.

Die Impedanz, die mit Z bezeichnet und in Ohm gemessen wird (Ω), ist ein AC-Äquivalent des Widerstands in Gleichstromkreisen. Sie ist in allen Komponenten aller Stromkreise vorhanden. Sie kann durch vektorielle Addition von Widerstand (siehe unten) und Reaktanz oder durch die Formel S = I²Z berechnet werden.

Die Beziehung zwischen Widerstand, Reaktanz und Impedanz ist analog zum Leistungsdreieck:

Z² = R² + X²

Perfekte Widerstände haben einen Widerstand ungleich Null, aber keinen Blindwiderstand. Perfekte Induktivitäten oder Kondensatoren haben einen Widerstand von Null, aber eine Reaktanz ungleich Null. Alle Komponenten einer elektrischen Schaltung besitzen eine gewisse Impedanz.

Letztes Update des Artikels: 5. Februar 2024